Appendix Two

A More Advanced Look at Current

In keeping with my promise not to bog you down with a lot of complex math I chose not to include many complex formulae in the main text. Indeed there are some topics that I left out that a traditional teacher of electricity or physiology would gnash his teeth at.

Much of the material in this book has been stripped A More down to just the bare essentials needed to understand electrical play. I did want to, however, include this one selection as an option just to show the more motivated reader:

1) How fast things can get complicated

and

2) That there are ways of producing reasonably accurate models of even the most complex electrobiological operations.

The topic well tackle is how currents distribute themselves in a conducting medium such as salt water or inside the human body. I won’t show the complex math involved, but I will discuss the limitations of the model.

Remember the carbon block example in Chapter 2 (page 19, figure 5)? What happens in the carbon block is the same thing that happens in the salt water thought experiment. There are many current paths available. But, let’s go back to the thought problem I set forth in Chapter 11 (P 85) – the high power line in the San Francisco Bay and the swimmer in Australia. We discussed verbally why the Australian swimmer does not get electrocuted. But is there a best or even a better way to show this? There are answers, but you won’t like what you have to do in order to get to them (unless you love math).

The best way to do it is to actually take an ocean and to measure the voltages and currents in different parts of it. This, however, requires very special and very expensive voltmeters and ammeters and, of course, scuba gear. A better way of doing ft is by making a mathematical model of the ocean as far as electric current is. The first trouble with that is that it’s a model and models have limitations. The second trouble is how close the model is to the real thing.

Imagine if the ocean were thinner than a sheet of paper (which of course it isn’t). Then I could have what’s known as a lattice resistance network, as shown in figure 36. The value of each of the resistors would be 2,000 ohms.

You’ll notice that the further I go from San Francisco, the more resistors the current must go through (even though they’re in parallel). I’ll save you the math (but, unfortunately, I can’t avoid it) and tell you the results. With 120 volts at San Francisco and the circuit as shown, the current in the first loop, Loop #1, is about 22 ma (milliamps). At about the 9th loop out, Loop #9, the current is already at 1/2 microamp. At the hundredth loop, Loop #100, the current is down to about one electron passing through the Australian swimmer every 100 billion billion billion years.

Now, how real is this model? I can t really tell you. But it does show that the current rapidly diminishes the further away from a voltage source it is. That’s the chief benefit from this particular model.

I can also make a highly simplified math model such as in figure 37, which is similar to the ocean model. Here Pm including a resistance for the skin of 10,000 ohms and a internal body resistance of 2,000 ohms. At Loop #1 the current is about I ma (mill lamp), and it falls to less than 1 µa (microamp) at Loop #8. Even if I change the voltage to 120 volts, the current at Loop #8 is still less than 1 µa (microamp). But how big physically are the loops themselves?

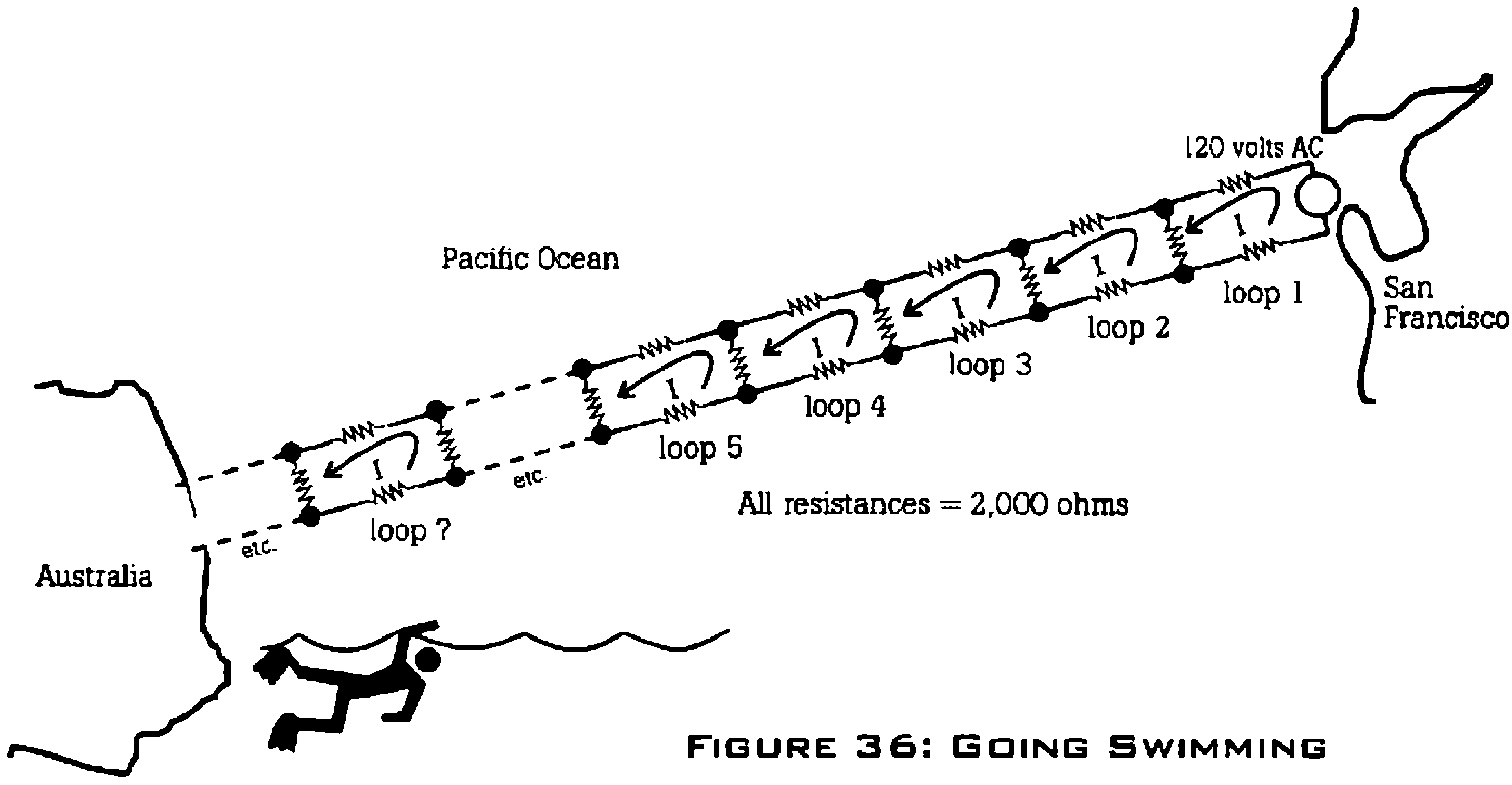
Figure 36: Going Swimming

Is this a good model? Car I still get results from it? The answer for all is, “I don’t know.” The only results you can derive from these models strongly suggests that the inner currents inside the body rapidly diminish away from the main current path.

Figure 37: Going Playing