 Help Wanted:
Help Wanted:
1. Mistake correction
2. Drawing illustrations in vector
Mistake in the text? Select it and click CTRL + ENTER
 Help Wanted:
Help Wanted:
1. Mistake correction
2. Drawing illustrations in vector
“Electricity and electrical phenomena” intoned the physics professor to a group of college students, “have not been really explained despite all our scientific c sophistication. We can describe its effects, bat we really don’t know what It is,” he concluded.
Seeing a student dozing in the hock row the professor roared, “Perhaps that young man back there can tell us what electricity is.” The student, not wanting to admit his inattention , stammered, “Gosh, professor, I did know it, bat I seem to have forgotten.” The professor throwing up his hands in mock frustration bellowed, “The only man in the universe who knows what electricity is… and he forgets!”
This little story was told to me by one of my professors in engineering school. It illustrates what we both know and don’t know about electricity. We really don t know what electricity is or what magnetism is and why electrical and magnetic fields interact. (Modern physicists will start talking about subatomic physics and quarks and the like, but you don’t need to go that deep.) All we do know about electricity are the effects, and we can describe these with a high degree of accuracy. That’s enough for our purposes.
What scientists and engineers know about electrical play is even less than what they know about electricity. Why? Because many of the electrical devices we pervs use for play were never designed for play. Often – owing to our creativity – the way we use standard electrical devices would void warranties if these uses were known.
To play with electricity, however, you really don’t need to be a rocket scientist. You do have to be aware of a few basic and simple rules. Someone’s life depends on your knowing and understanding these rules.
Remember what I said in Chapter 1 about electricity being edge play because “accidents can happen faster than you can respond to them”? Let me now illustrate this point with a simple physics experiment. You’ll need to work with a friend on this.
 Electricity travels faster than human reflex. If something goes wrong during electricity play, it’ll probably happen too fast for you to stop it.
Electricity travels faster than human reflex. If something goes wrong during electricity play, it’ll probably happen too fast for you to stop it.
Have your friend take one of your pieces of currency, (Make it a $100 bill – a fresh one – so that both of you will really be motivated.) Have your friend hold the bill between your open thumb and forefinger as shown in fig. 1.
Your challenge is to catch the bill with your fingers as soon as your friend releases the bill from her fingers. (Don’t cheat and try to grab it while it’s still in your friend’s fingers.) To add some extra incentive for both of you, let your friend keep any bills that fait to the floor.
Now let me be the Great Carnak. I predict that despite how fast you are, all bills will drop to the floor. (I can’t predict, however, whether your friend will remain a friend.)
Why is this so? Physics – well, really, physiology and physics.
The bill is affected by gravity, and its falling acts in accordance with a well-known formula developed by Sir Isaac Newton more than 300 years ago. (Consult a high school physics text for the formula.) This formula tells us that it takes about 180/1000ths of a second (that’s 180 milliseconds) for the bill to completely clear your fingers.
Experiments in physiology, however, show that the time for a person to respond from eyeball sighting to finger damp is about 250 milliseconds. Not even close. If you don’t believe me, try it for yourself. Really, I’d strongly suggest you try this with a friend. (Can I be your friend?)
This simple experiment will give you a physical sense of the times involved and give you some confidence that fi Uncle Abdul, know whereof I speak.
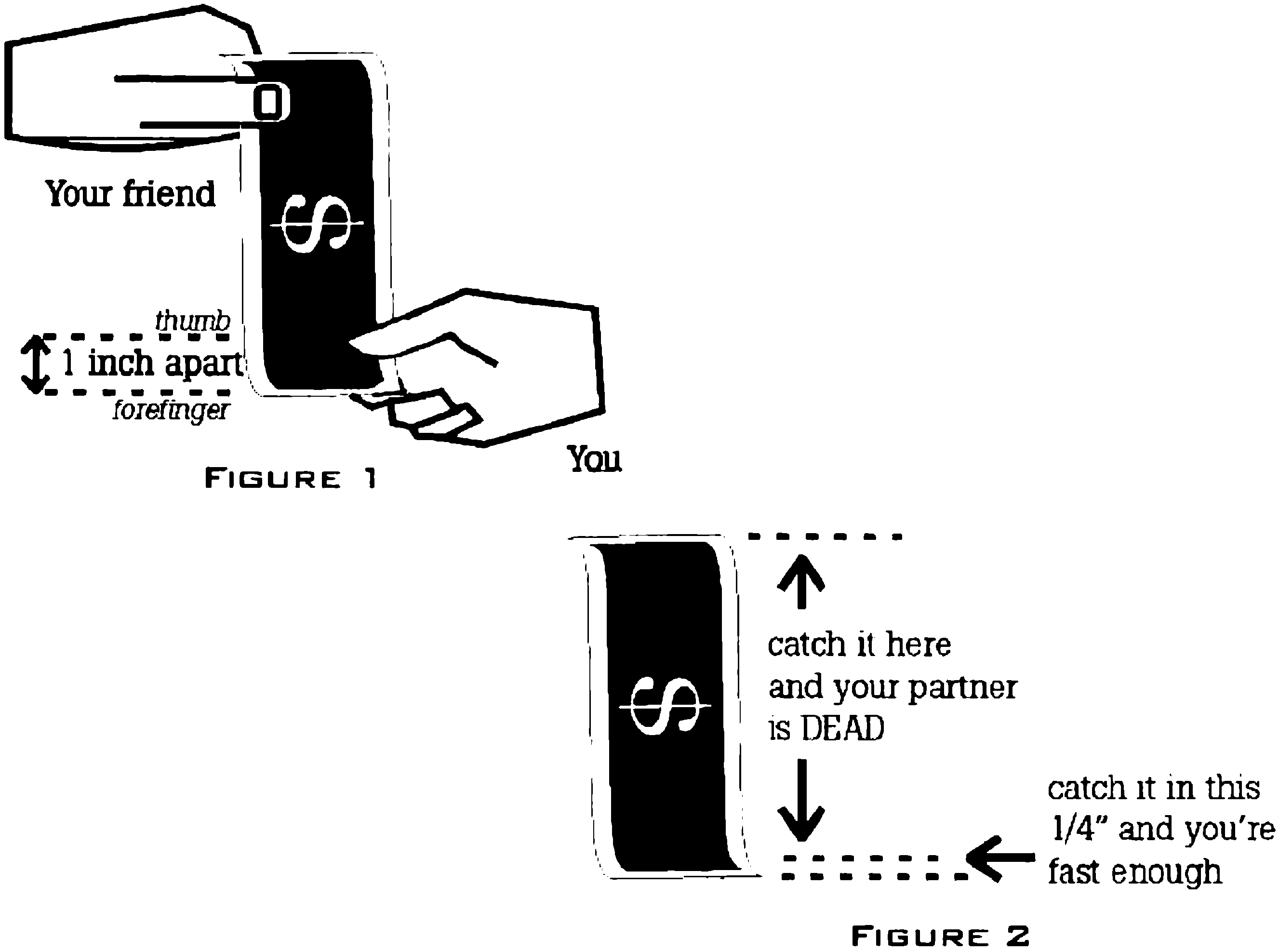
Figure 1 / Figure 2
So what does this game have to do with electrical play? Well, gentle reader, other physiological experiments and studies have shown that it can take 10 milliseconds (msecs.) or less to cause death in a human being due to electrical damage. You might be able to train yourself to be able to catch the bill, but even that won’t be fast enough (unless you can catch it in the first quarter-inch). You can’t react fast enough to prevent injury or death in electrical play (see figure 2).
So much for gruesome illustrations; how about some practical physics?
To start your understanding of the physics of electricity, let’s look at the concepts of Voltage, Current, and Resistance and how they are related.
Let’s start with voltage. Voltage is usually represented in electrical formulas by the letter “E” (or, in some texts, “V”) and is measured in (oddly enough) volts by (odder still) a thing called a voltmeter.
To find out what voltage is, let’s do a “thought experiment” – the best way to do this one.
Think about taking your clothes iron, and holding it directly over your head a s high as you can reach. Your iron has the “potential” of giving you a very bad headache (or even death under certain circumstances) if you let it go. Nothing happens if nothing moves.
 Voltage is the “potential” of electricity: how much power it will have if it starts to move. Imagine water in a bucket – the height you hold it above the ground is voltage.
Voltage is the “potential” of electricity: how much power it will have if it starts to move. Imagine water in a bucket – the height you hold it above the ground is voltage.It’s not voltage that kills, but it helps. You have to know where it is and where and how things will move.
The “thing that moves” is called current, represented by the letter “I.” It is measured in amperes or amps by something called an ammeter.
 Current is the “stuff” of electricity. If that closed container of water were connected to a pipe so it could flow, the flow of the “water” would be current.
Current is the “stuff” of electricity. If that closed container of water were connected to a pipe so it could flow, the flow of the “water” would be current.What is current? Current is the “stuff” – usually electrons – that moves through a conductor when a potential, voltage, is applied across that conductor. By the convention we use in this book, conventional current flows (moves) from a higher voltage to a lower voltage. In a battery that would be from the positive, “+” terminal, through the conductor to the negative, “-”, terminal.
R, now, stands for resistance measured in ohms. You can use an ohmmeter if you want to measure it, but you’ll learn that you don’t really need one.
What is resistance? Resistance is the resistance to the flow of current. To illustrate, consider driving a nice open freeway. With the traffic moving well you can go 55 (unless the cops aren’t around). But have an obstruction – like rubberneckers at an accident – and your speed or “flow” is reduced.
 Resistance is bow hard or easy it is for current to flow through a given substance. The diameter of the pipes through which the “water” flows is resistance. (The bigger the pipe, the lower the resistance.)
Resistance is bow hard or easy it is for current to flow through a given substance. The diameter of the pipes through which the “water” flows is resistance. (The bigger the pipe, the lower the resistance.)Current will flow through any material – copper wire, electrical resistors, seawater wood, plastic, even skin, muscle, and blood. We can say then that all materials have a resistance. Those with low resistance – say copper wire – are generally called conductor. Those materials with high resistance – say such as wood, air, fresh water or skin – are called insulators. What about those materials whose resistance is between those two – like carbon, muscles, etc.? Well, they’re called conductors or insulators, depending on what they’re being compared to.
 Voltage is measured in volts, represented by the letter E. Current is measured in amps, represented by the letter I. Resistance is measured in ohms, represented by the letter R.
Voltage is measured in volts, represented by the letter E. Current is measured in amps, represented by the letter I. Resistance is measured in ohms, represented by the letter R.Understand all the above? Good!
Now let me give you two laws that well frequently use to understand electrical play.
The first of these laws is called Ohm’s Law. Ohm’s Law says that E = IR, or that voltage is equal to the product of current and resistance. Remember that from high school physics? No? Well, an easier way to remember and use it is by looking at figure 3. As shown in the figure, cover any one of the letters, and you’ll be told how to find it in terms of the other two. This is really the most important formula in electricity because it’s so very useful. For any linear material like copper wire, Ohm’s Law holds.
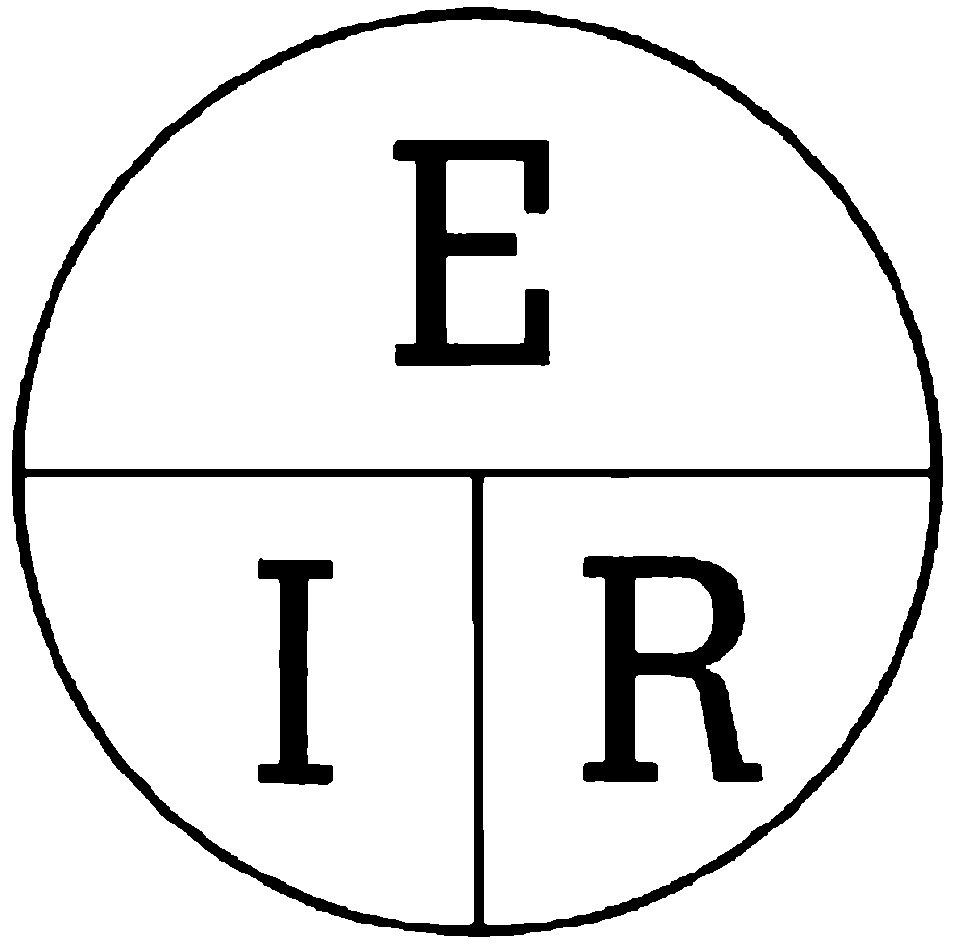
Fig.
3 – The Ohm’s Law Circle
Let’s try an example. Go back to figure 3. If you have a 9-volt battery (E = 9 volts) connected across a 100.000 ohm conductor (R = 100,000 ohms), what would be the current, I, in amps?
You’re looking for I in the circle in figure 3. Cover it with your finger. You see that E is over the R. That means that you find 1 by taking the value for E (9 volts) and dividing it by the value for R (100,000 ohms). The value you get for I is 9/100,000 amperes (or amps). It’s a lot easier to say 90 microamps (μa) [I microamp (μa) = millionth of an amp] or 0.09 ma (mijliamps).
 Ohm’s Law says that you can calculate voltage, current or resistance if you know the other two.
Ohm’s Law says that you can calculate voltage, current or resistance if you know the other two.As an interesting historical footnote, Gregg Ohm, the German physicist who developed the law t wrote in the very same scientific paper a complaint about his impoverished state as a physicist I guess he was saying, “Will Discover Electrical Laws For Food.”
The other law is called Kirchhoff’s Law, Kirchhoff’s Law tells us about some conventions for looking at currents and voltages in circuits so you can calculate them mathematically. Since HI be doing some simple math examples in this book, you’ll need to understand the law a little bit.
 Kirchhoff’s law says that “what goes in comes out” – that the sum of currents leaving one part of a circuit is equal to the sum of currents coming into another part.
Kirchhoff’s law says that “what goes in comes out” – that the sum of currents leaving one part of a circuit is equal to the sum of currents coming into another part.There are many ways to state Kirchhoff’s Law. For this book, the first important thing to know is that the current that goes out of one terminal of a voltage source (such as a battery’s + terminal) is the same as the current coming in at the other end (the – terminal). This is true even if you have more than one voltage source and/or more than one resistor: the total current that goes into the system is the same as the total current that comes out.
There are two spinoffs of Kirchhoff’s Law.
Take a look at figure 4. It shows a voltage source (in this case a 9-volt battery) connected across two conductors. This type of connection is called a parallel resistance circuit. One conductor (R1) has a resistance of 2,000 ohms, the other (R2) 1 ,000 ohms. Using figure 3, we calculate that the current through conductor R1 is 9/2000 amps or 4.5 ma. The current through conductor R2 is 9/1000 amps or 9 ma. The battery and the two resistances are connected at a junction. Since the current going into the junction is the same as the current going out of the junction, the voltage source is delivering 4.5 + 9 ma or 13.5 ma., the sum of the two currents.
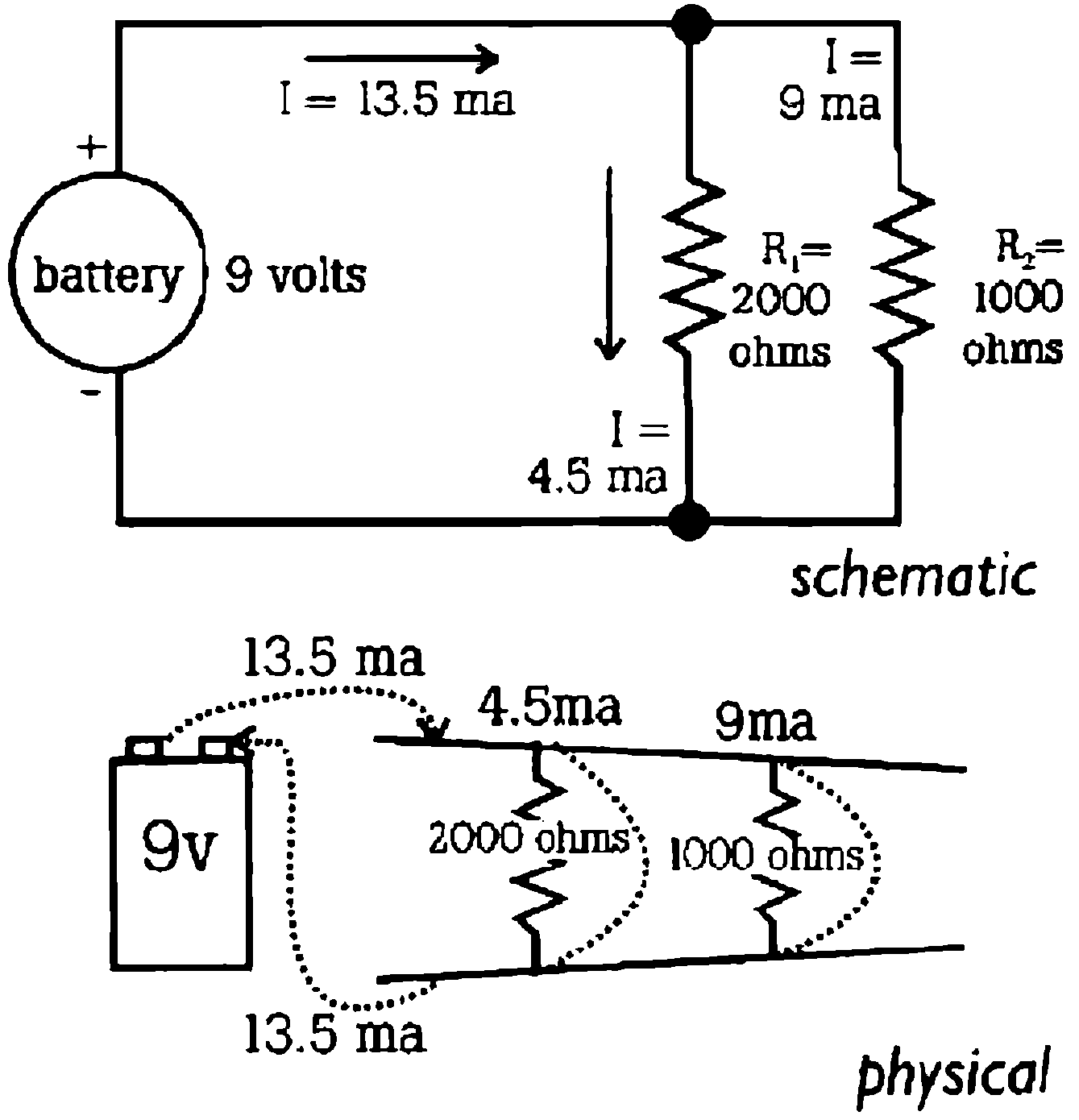
Figure 4: Two Views of Parallel Circuit
Now take a look at figure 5. The same two conductors, R1 = 2,000 ohms and R2 = 1,000 ohms, are connected end-to-end and both are across the battery (E = 9-volts). We call this connection a series connection.
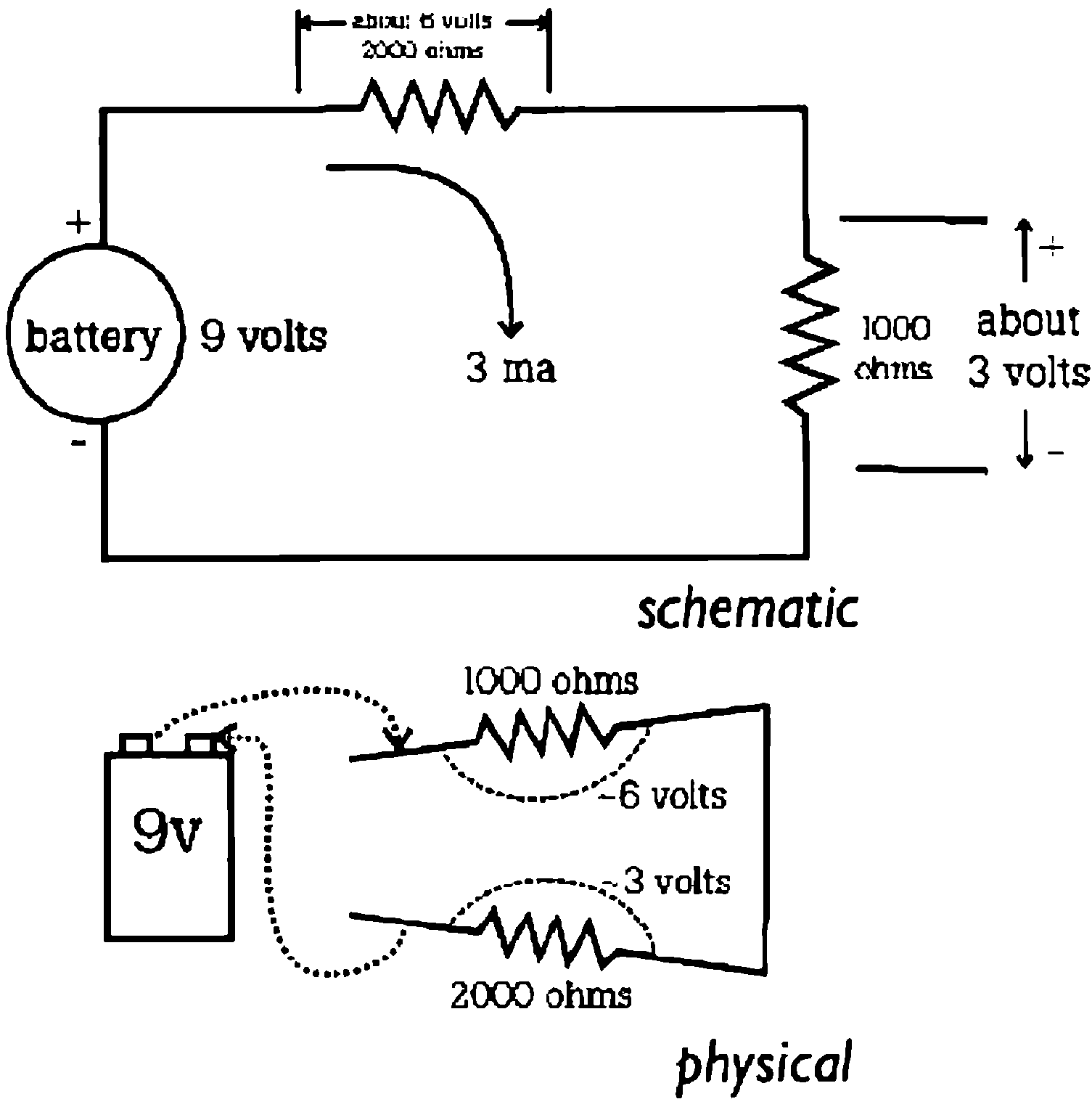
Figure 5: Two Views of Series Circuit
Kirchhoff’s Law, “current out equals current in,” means that you can’t have a different current through R1, than you do R2. Since the current has to be the same (in this case we’ll call it some unknown value, I) figure 3 would show that the voltage across R1, would be 2000 x 1. The voltage across R2 would be 1000 x 1. The two voltages would have to equal the battery’s voltage of 9 volts. They would have to add up. So,
9-volts (battery) = (2000 x l)[across R1] + (1000 x l)[across R2]
If you do the math right, you get:
9-volts (battery) = (2000 + 1000) x I [across both R1 and R2]
In other words the resistances of the conductors in a series connection are added together So, the total resistance of the conductors connected in series, R( total), is
R(total) = R1 + R2
R(total) = (2000 ohms + 1000 ohms) = 3000 ohms.
Using figure 3 again, we find the current, I, to be 9/3000 amps or 3 ma.
Let’s use figure 3 again. With R1 = 2000 ohms and I = 3 ma, we find that the voltage across R1 (what you would measure if you put a voltmeter across R1) is 6 volts. Similarly, the voltage across R2 is 3 volts. 6 volts + 3 volts is 9 volts – the same as the battery voltage. Wow! That was lucky. Not luck really, just physics.
Kirchhoff’s Law is the second most used law in electricity. It’s used to study and design electrical circuits – circuits like the one that runs across a nipple, or through an electrical toy.
The concepts of voltage and current are fine when you’re dealing with electrical circuits such as you find in a toaster, an electrical toy, or house wiring. But what if you’re dealing with a block of material like a block of carbon or even a human body?
If you’re looking at the material as a single lump with one wire going into it and one coming out, then you can think of the material as a single resistor with a resistance. But if you’re wondering what the voltage or current is like inside the material, you need to expand the concepts of voltage and current a little. You’ll understand the need for this when we look at currents and voltages inside the human body in later chapters.
Let’s start with current first.
If I connect a battery across two opposite corners of a cube of carbon (see fig. 6), the current going into and out of the battery and through the wires will be the same. But inside the carbon cube, the current can take any number of paths from one corner to the other.
 If current is running through something three-dimensional, the greatest amount of current will run through the most direct route, but smaller amounts will run through other routes.
If current is running through something three-dimensional, the greatest amount of current will run through the most direct route, but smaller amounts will run through other routes.Current density is defined as “the current flowing per unit area.” Its units are usually measured as amps per cubic centimeter (or some other standard three-dimensional measurement). An easy way to think about this is to imagine dividing your material up into evenly sized “chunks” and measuring how much current flows across each one.
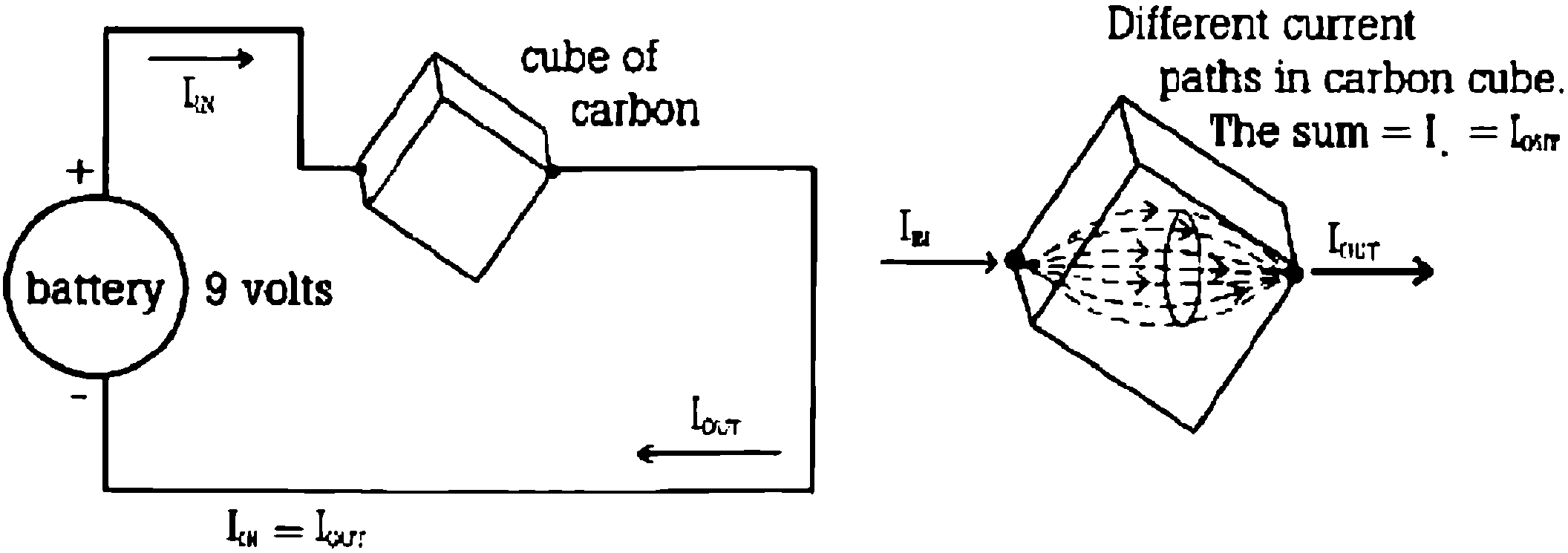
Figure 6: Current Through a Carbon Cube
Another way to think of this concept is to envision that the electrons coming out of the wire can now take any path inside the material, but that they generally go from the point of input to the point of output. Thus, if you take any one or a group of these paths and count the number of electrons going through it in one second, you’ll have current density. Current density is usually consistent throughout a linear material – a solid chunk of a single substance.
We’ll be using current density concept when we look at what happens when current flows inside a body during electrical play, so this is more than a “me genius, you student” exercise.
Now, let’s take a look at a concept extension for voltage.
This new concept is called voltage gradient, You can best see it by looking at figure 7.
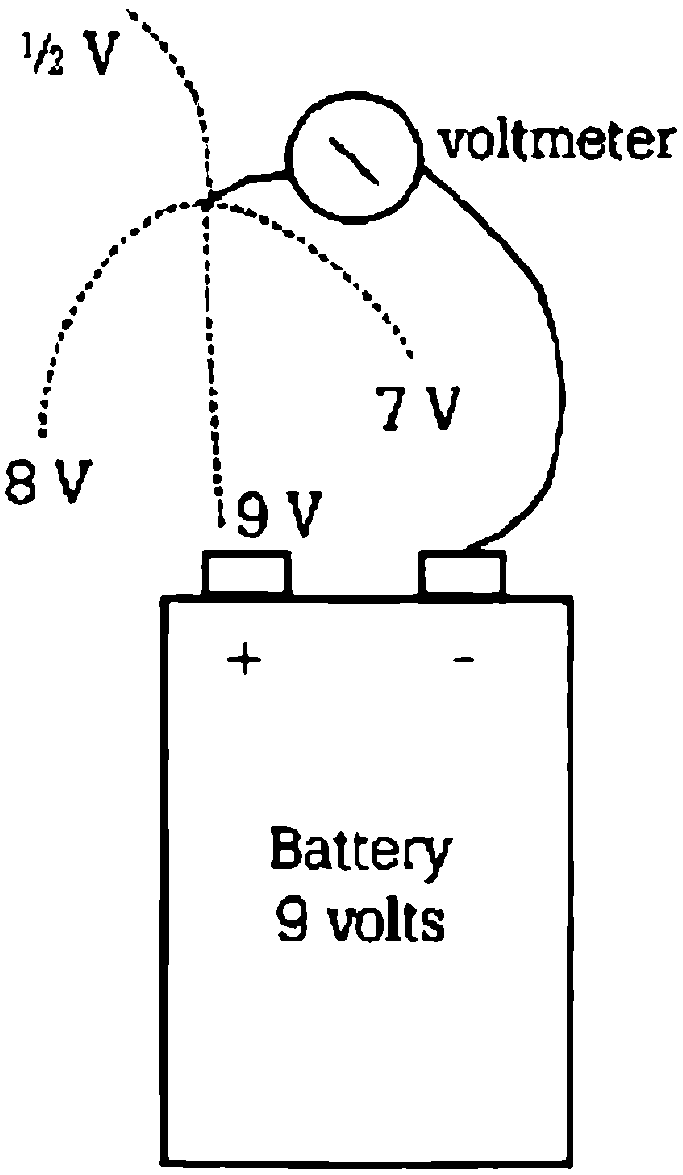
Figure 7: Voltage Gradient
If I had a battery sitting out in the air and had a sensitive enough voltmeter, I could measure the voltage across the battery terminals (of course). But I could also measure voltage anywhere in the air close to or far away from the battery. This is called an electric field.
Again – like with current density – you can generate a complex resistance circuit to model a voltage gradient or an electric field for mathematical analysis. But the general concept is especially useful when we discuss static electricity.
This is a question you may be asking now. After all it seems the whole world runs on household AC voltage. Why, even some of our play toys get plugged into the wall. What about it, Unc?
I’m not forgetting it. AC or alternating current does indeed run the whole world. When you have a network of power stations, AC provides a means of easily distributing the power.
 Alternating current, the kind found in household wiring in the U.S., switches rapidly back and forth from one direction to the other.
Alternating current, the kind found in household wiring in the U.S., switches rapidly back and forth from one direction to the other.DC or direct current is what you get from batteries or DC power supplies. In DC the current only flows in one direction – “+” to “-”. If the current flows, then stops, then flows, but still in one direction, this would be called pulsed or interrupted DC current.
AC simply means that in a circuit, current first flows in one direction, then it reverses and flows in the opposite direction. This of course means that the voltage changes polarity (+ and -) at the same time. If the circuit devices can store current (a flow of electrons, remember), then the math becomes more complicated. However, all the definitions and laws I talked about above still apply. It’s just that the math gets to be more fun.
Does this mean we pack it in? No. Fortunately, the human body acts almost entirely like a resistor and hardly stores any current, so we can treat AC on the body the same as if it were DC. Whew! That’s lucky.
In the book there will be some places where I’ll have to give you some information that is unique to AC. I’ll leave out the math, yet try to be dear enough that you can understand the concepts presented.
One important thing about AC is the term Hertz (or Hz). This isn’t what electricity does when you run it across a scrotum – it’s the number of times per second or frequency that the voltage (and thus the cur rent) changes in one second. Household AC current has a frequency of 60 Hz (Hertz), Here we mean that the voltage changes 60 times in a second. Television signals are at 1 00,000,000 (or 1 00 mega) Hz (Hertz).
This completes our discussion of the electrical definitions and laws that we’ll need in this book.
Oooops…
You’ve probably heard of the wise man’s saying, “All rules, including this one, are false”. The final law is a little like that. We can say it as follows: “There is no such thing as ‘linear’ in nature”.
Remember earlier in this Chapter when I said that, “For any linear material like copper wire or an electric heater. Ohm’s Law holds”? Well, no material in nature is completely linear, not even a good conductor like copper wire. There are always impurities, variations in breadth, or something else that makes your calculations just a little bit less reliable. (That’s kind of the way life is – no sooner do you think you understand the rules when someone comes up with new information.)
Does that mean we pack it in – again? No, it just means you have to be careful in how you use these laws. You have to know and understand what the limits of the law are and when and where they can be applied. Most S/M players have developed a basic understanding of what “limit” means.
The next chapter will take a look at some of these limits.