Help Wanted:
1. Mistake correction
2. Drawing illustrations in vector
Mistake in the text? Select it and click CTRL + ENTER
Help Wanted:
1. Mistake correction
2. Drawing illustrations in vector
Old Vaudeville joke about Cases –
A man sees a lawyer walking down the street carrying a brand new brief case . The lawyer says, “I’m taking my cast to court.”
The following week, the man sees the some lawyer carrying the same briefcase and a ladder. The lawyer now says, “I’m taking my case to a higher court.”
Before we leave Messrs. Ohm and Kirchhoff and definitions, lets go through four special circuit cases. More than just practice exercises, these cases will closely approximate real-world situations you’ll run across in electrical play.
In the first model we show a series circuit in which R1 = 100 ohms, R2 = 100,000 ohms, and E = 9 volts.
Take a look back at figure 5 on page 17. In that figure, you can see that Rtotal = R1 + R2 : 100 + 100,000 = 100,100 ohms. If you go back to figure 3 (p. 15), the Ohm’s Law Circle, you can see that I = 9/100,100 or 8.991008991 microamps (µa) or damn near 9µa.
Use Ohm’s Law again to find the voltage across R1: 0.008991008991 volts, or damn near 0 volts. Similarly, the voltage across R2 is 8.99 1 00899 1 volts – that’s 9 volts to you (or to me).
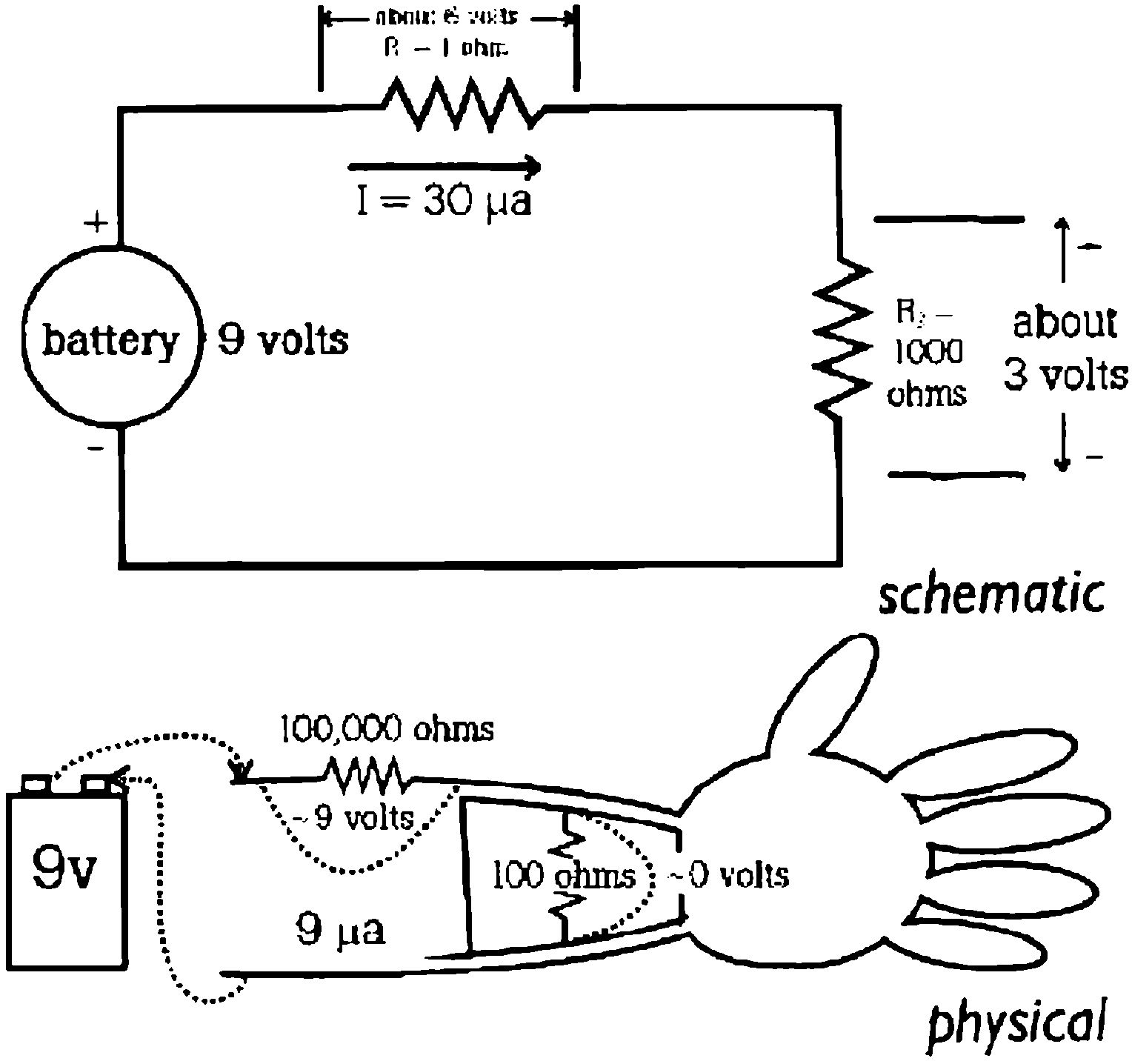
Figure 9: Two views of electricity, outside & in
Apart from a re-confirm at ion of the first special case, what does this case mean?
Weil, here we are dealing with typical values found in electrical play. Nine-volt batteries are used in such electrical toys such as TENS units. 100,000 ohms is usually considered a good safe value for the resistance of human skin, Note that unbroken skin resistance can vary from 10,000 to 1,000,000 ohms, but 100,000 ohms is considered to be a good dry, unbroken skin resistance value for toy design and safety design purposes. (Remember limits to models?) 100 ohms is a general value that is used for the resistance of body stuff – muscles, blood, etc. – that lie below the skin. Again this varies, but 100 ohms is commonly accepted.
In a circuit with several different resistances in series, the highest determines the current. Since un broken skin has high resistance, it often determines the current in electricity play.Now, let me ask you a question. Why is unbroken skin so important?
tah-dah-dum-de-de-de-dum-dum-dum…
Got your answer? Good, let s check it.
From the first case we see that the largest resistance in a series circuit determines the current in that circuit. In Figure 9, represents dry, unbroken skin, which dictates the current that runs through the bottom’s body, Thanks skin! Wei I get back to this later, but I hope you’ll understand a very important idea here.
And you thought that studying electricity was going to be dull, uninteresting, or too much over your head.
Let’s look at other skin resistance values.
Now look at the circuit shown in figure 11. This is yet another series connection circuit where E = 9 volts, but R1 = 10,000 ohms and R2 = 100 ohms. Using Ohm’s Law, we find the current, I = 891 microamps (µa). The voltage reduction across R1 is 8.9 volts. The voltage reduction across R2 is 0.1 volts.
Figure 10: Two Views of Circuit with Sweaty Skin
Here we notice again that the current is limited by the skin resistance, but that the lower the skin resistance gets, the higher the current in the body gets. Skin resistance lowers when a person gets sweaty But also note that the current in case 4 is near 1,000 microamps (µa) or about I miliiamp (ma). We’ll see later that this is about I/10th the usual danger value of current. So we can see that we can usually – but not always – depend on the protection of skin during electrical play.
Take a look at the circuit shown in figure 11. Once again another series connection circuit where E = 9 volts, but R1 = 100 ohms and R2 = 100 ohms. Using Ohm’s Law, we find the current, I = 45 ma. The voltage drop across R1 is 4.5 volts. The voltage drop across R2 is 4.5 volts.
Sweaty skin has lower resistance than dry skin. Broken skin has lower resistance than intact skin. The interior of the body has lower resistance than any skin.This figure, of course, represents what would happen if the probe of an electrical toy ever got below the surface of the skin and inside the body. A current of 45 ma inside the body is definitely dangerous. Again we see the importance of skin.
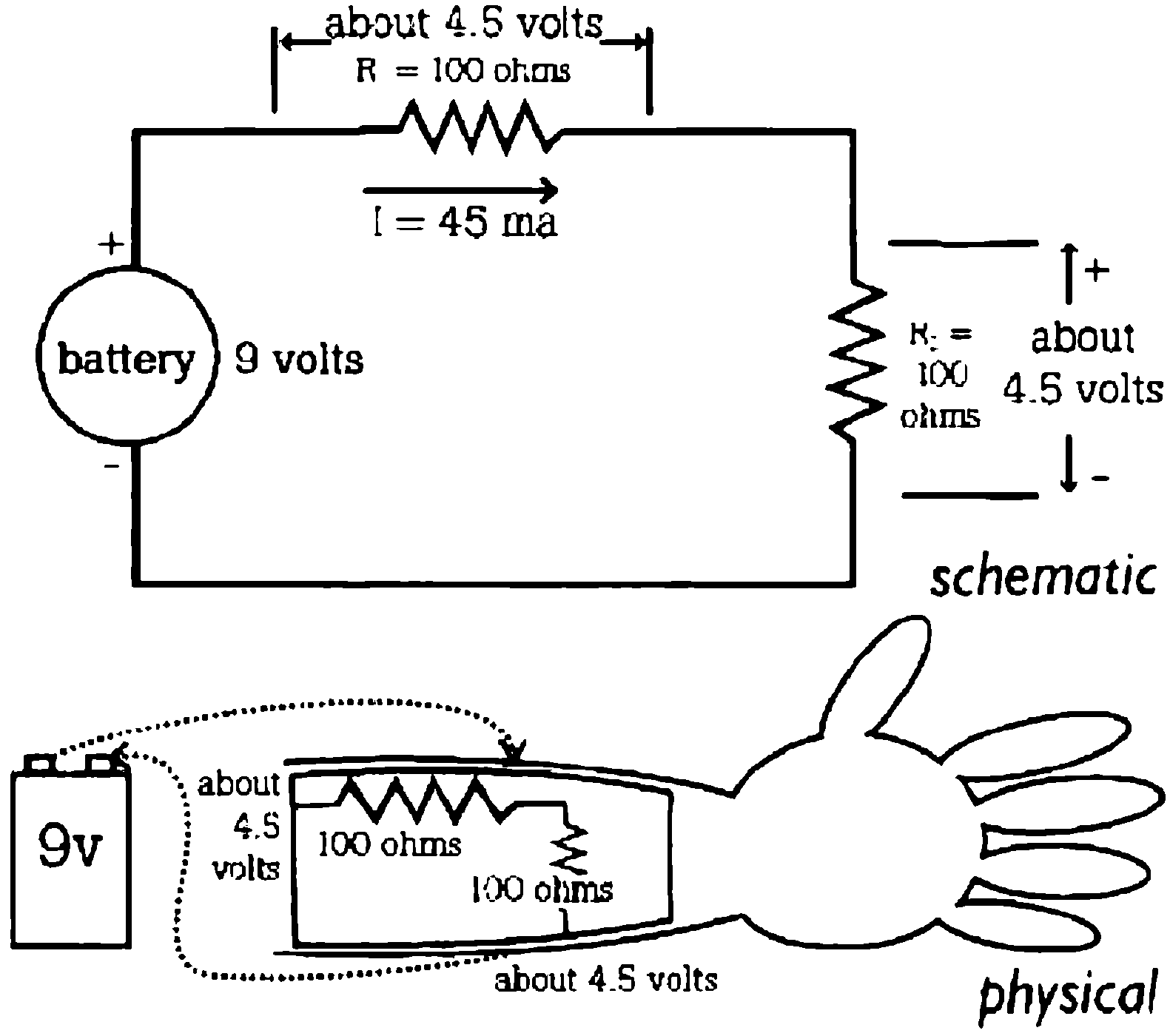
Figure 11: Two views of circuit inside body
Figure 13 looks at what happens when you put a low parallel resistance, R2, across a high resistance, R3 + R4. If you have a good understanding of Ohm’s and Kirchhoff’s Laws, you should get the same results I show in the figure.
Why is this important? Well, in upcoming chapters on electrical safety, you’ll see that many safety devices use a low-resistance “shunt” (represented by R2) across “you” (represented by R3 and R4). This allows most of the current to go through the lower resistance – so that much less of it goes through “you.”
Figure 12: Two Views of Safety Shunting
I’m trying to demonstrate that you car solve many of the practical problems of electrical play by using relatively simple models. You also begin to see, I hope, that these models can help with explanations as long as you understand that they have limits.
Now, let’s move on.